Question

A gas contained within a piston-cylinder assembly, initially at a volume of 0.1 m^3, undergoes a constant-pressure expansion at 2 bar to a final volume of 0.12 m^3, while being slowly heated through the base. The change in internal energy of the gas is 0.25 kJ. the piston and cylinder walls are fabricated from heat-resistant material and the piston moves smoothly in the cylinder. The local atmosphere pressure is 1 bar.

a.) For the gas as the system, evaluate the work and the heat transfer, each in
b.) For the piston as a syatem, evautate the work and change in potential energy, in kJ.

Answer 1

Answer: (a). W = 4KJ and Q = 4.25KJ

(b). W = -2KJ and ΔPE = 2KJ

Step-by-step explanation:

(a).

i. We are asked to calculate the work done during the expansion process considering gas as system.

from W =
`\int\limits^a_b {p} \, dV` where a = V₂ and b = V₁

so W = P(V₂-V₁)

W = (2 × 10²) (0.12 - 0.10)

W = 4 KJ

ii. We apply the energy balance to gas as system

given Q - W = ΔE

Where ΔE = ΔU + ΔKE + ΔPE

since motion of the system is constrained, there is no change in both the potential and kinetic energy i.e. ΔPE = ΔKE = 0

∴ Q - W = ΔU

Q = ΔU + W

Q = 0.25 + 4

Q = 4.25 KJ

(b).

i. to calculate the work done during the expansion process considering piston as system;

W =
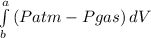`\int\limits^a_b {(Patm - Pgas)} \, dV`where a and b represent V₂ and V₁ respectively.

W = (Patm - Pgas)(V₂ - V₁)

W = (1-2) ×10² × (0.12-0.1)

W = -2KJ

ii. We apply the energy balance to gas as system

given Q - W = ΔE

Where ΔE = ΔU + ΔKE + ΔPE

Q = 0 since the piston and cylinder walls are perfectly insulated.

for piston, we neglect the change in internal energy and kinetic energy

ΔU = ΔKE = 0

from Q - W = ΔU + ΔKE + ΔPE

0 - (-2) = 0 + 0 + ΔPE

∴ ΔPE = 2KJ