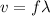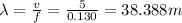Answer:
Wavelength will be 38.388 m
Step-by-step explanation:
We have given mass m = 13.9 kg
Spring constant K= 9.3 N/m
Velocity v = 5 m /sec
Angular frequency is given by
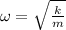
So
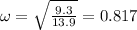
Now we have to find frequency for further calculation
So frequency will be equal to

Now we have to find wavelength, it is ratio of velocity and frequency
There is a relation between frequency velocity and wavelength