Question

A space vehicle is traveling at 5000 km/h relative to the Earth when the exhausted rocket motor is disengaged and sent backward with a speed of 71 km/h relative to the command module. The mass of the motor is four times the mass of the module. What is the speed of the command module relative to Earth just after the separation?

Answer 1

The speed of the command module relative to earth just after the separation is 4985.8 km/h

Step-by-step explanation:

Given that,

Velocity of vehicle = 5000 km/h

Relative velocity = 71 km/h

The mass of the motor is four times the mass of the module.

We need to calculate the velocity of motor

Using formula of relative velocity

`v=v_(2)-v_(1)`

Put the value into the formula

`71=v_(2)-v_(1)`

`v_(2)=71+v_(1)`

We need to calculate the speed of the command module relative to Earth just after the separation

Using conservation of momentum

`mu=m_(1)v_(1)+m_(2)v_(2)`

Put the value into the formula

`5m*5000=4m* v_(1)+mv_(2)`

`5*5000=4* v_(1)+(71+v_(1))`

`25000=5v_(1)+71`

`v_(1)=(25000-71)/(5)`

`v_(1)=4985.8\ km/h`

Hence, The speed of the command module relative to earth just after the separation is 4985.8 km/h

Answer 2

the speed of the command module relative to Earth just after the separation = 4943.2 Km/hr

Step-by-step explanation:

Given:

speed of space vehicle =5000 km/hr

rocket motor speed = 71 km/hr relative to the command module

mass of module = m

mass of motor = 4m

By conservation of linear momentum

Pi = Pf

Pi= initial momentum

Pf= final momentum

Since, the motion is only in single direction

`MV_i=4mV_(mE)+mV_(cE)`

Where M is the mass of the space vehicle which equals the sum of motor's mass and the command's mass, Vi its initial velocity, V_mE is velocity of motor relative to Earth, and V_cE is its velocity of the command relative to Earth.

The velocity of motor relative to Earth equals the velocity of motor relative to command plus the velocity of command relative to Earth.

V_mE = V_mc+V_cE

Where V_mc is the velocity of motor relative to command this yields

`5mV_i = 4m(V_(mc)+V_(cE))+mV_(cE)`

`5V_i = 4V_(mc)+5V_(cE)`

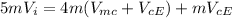
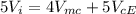
substituting the values we get

`V_(cE) = (5V_i-4V_(mc))/(5)`

`V_(cE) = (5(5000)-4(71))/(5)`

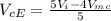
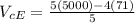
= 4943.2 Km/hr

the speed of the command module relative to Earth just after the separation = 4943.2 Km/hr