Answer:
(A) Maximum voltage will be equal to 333.194 volt
(B) Current will be leading by an angle 54.70
Step-by-step explanation:
We have given maximum current in the circuit
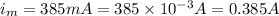
Inductance of the inductor
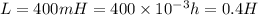
Capacitance

Frequency is given f = 44 Hz
Resistance R = 500 ohm
Inductive reactance will be
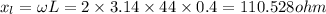
Capacitive reactance will be equal to
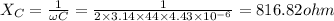
Impedance of the circuit will be
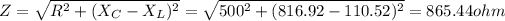
So maximum voltage will be
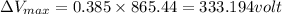
(B) Phase difference will be given as
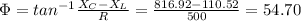
So current will be leading by an angle 54.70