Answer:
5.994 V
Step-by-step explanation:
The pressure as a function of hoop strain is given:
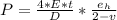

For wheat-stone bridge with equal nominal resistance of resistors:
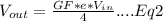
Hence, input Eq1 into Eq2

Given data:
P = 253313 Pa
D = d + 2t = 0.09013 m
t = 65 um
GF = 2
E = 75 GPa
v = 0.33
Use the data above and compute Vout using Eq3
