Question

Assume a strain gage is bonded to the cylinder wall surface in the direction of the hoop strain. The strain gage has nominal resistance R0 and a Gage Factor GF. It is connected in a Wheatstone bridge configuration where all resistors have the same nominal resistance; the bridge has an input voltage, Vin. (The strain gage is bonded and the Wheatstone bridge balanced with the vessel already pressurized.)Calculate the voltage change ∆V across the Wheatstone bridge when the cylinder is pressurized to ∆P = 2.5 atm. Assume the vessel is made of 3004 aluminum with height h = 21 cm, diameter d = 9 cm, and thickness t = 65 µm. The Gage Factor is GF = 2 and the Wheatstone bridge has Vin = 6 V. The strain gage has nominal resistance R0 = 120 Ω.

Answer 1

5.994 V

Step-by-step explanation:

The pressure as a function of hoop strain is given:

`P = (4*E*t)/(D)*(e_(h) )/(2-v)`

`e_(h) = (D*P*(2-v))/(4*E*t) .... Eq1`

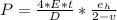
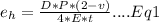
For wheat-stone bridge with equal nominal resistance of resistors:

`V_(out) = (GF*e*V_(in) )/(4) .... Eq2`

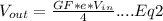
Hence, input Eq1 into Eq2

`V_(out) = (GF*e*V_(in)*D*P*(2-v) )/(16*E*t) .....Eq3\\`

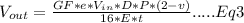
Given data:

P = 253313 Pa

D = d + 2t = 0.09013 m

t = 65 um

GF = 2

E = 75 GPa

v = 0.33

Use the data above and compute Vout using Eq3

`V_(out) = (2*6*0.09013*253313*(2-0.33) )/(16*75*10^9*65*10^-6) \\\\V_(out) = 0.006285 V\\\\change in V = 6 - 0.006285 = 5.994 V`