Question

At a medical center, a sample of 20 days showed the following number of cardiograms done each day.

25 31 20 32 13 14 43 12 57 23 36 32 33 32 44 32 52 44 51 46

(a) Find the sample mean x.

(b) Construct a stem and leaf plot for the data.

(c) Find the sample variance s^2 and the sample standard deviation

Answer 1

a) 33.6

b)

Stem Leaf

1 2 3 4

2 0 3 5

3 1 2 2 2 2 3 6

4 3 4 4 6

5 1 2 7

c)

Sample variance=174.57

Sample Standard deviation=13.21

Explanation:

a) The sample mean xbar is computed by adding all x's values and divided the resultant value to number of observation

sumx=25+31+20+32+13+14+43+12+57+23+36+32+33+32+44+32+52+44+51+46

sumx=672

sample mean=672/20=33.6

b) Firstly arranging the data into ascending order

12,13,14,20,23,25,31,32,32,32,32,36,43,44,44,46,51,52

Now making stem and leaf plot

Stem Leaf

1 2 3 4

2 0 3 5

3 1 2 2 2 2 3 6

4 3 4 4 6

5 1 2 7

The stems are 1,2,3,4 and 5. The leaves are 234,035,1222236,3446 and 127.

c)

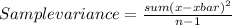
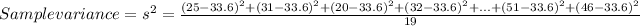
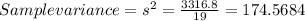
`Sample variance=(sum(x-xbar)^2)/(n-1)`

`Sample variance=s^(2) =((25-33.6)^2+(31-33.6)^2+(20-33.6)^2+(32-33.6)^2+...+(51-33.6)^2+(46-33.6)^2)/(19)`
`Sample variance=s^(2) =(3316.8)/(19) =174.5684`

Sample variance=174.57

`Sample standard deviation=√(Sample variance)`
`Sample standard deviation=s=√(174.5684) =13.21243`

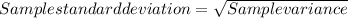
Sample standard deviation=13.21