Answer:
a) 33.6
b)
Stem Leaf
1 2 3 4
2 0 3 5
3 1 2 2 2 2 3 6
4 3 4 4 6
5 1 2 7
c)
Sample variance=174.57
Sample Standard deviation=13.21
Explanation:
a) The sample mean xbar is computed by adding all x's values and divided the resultant value to number of observation
sumx=25+31+20+32+13+14+43+12+57+23+36+32+33+32+44+32+52+44+51+46
sumx=672
sample mean=672/20=33.6
b) Firstly arranging the data into ascending order
12,13,14,20,23,25,31,32,32,32,32,36,43,44,44,46,51,52
Now making stem and leaf plot
Stem Leaf
1 2 3 4
2 0 3 5
3 1 2 2 2 2 3 6
4 3 4 4 6
5 1 2 7
The stems are 1,2,3,4 and 5. The leaves are 234,035,1222236,3446 and 127.
c)
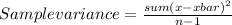
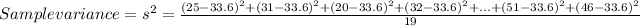
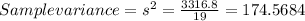
Sample variance=174.57
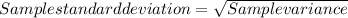
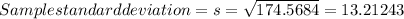
Sample standard deviation=13.21