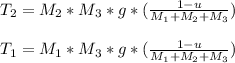Question

The system below uses massless pulleys and ropes. The coefficient of friction is μ. Assume that M1 and M2 are sliding. Gravity is directed downwards. Find the tension in the rope.

Answer 1

Step-by-step explanation:

Using Newtons second law on each block

F = m*a

Block 1

`T_(1) - u*g*M_(1) = M_(1) *a \\\\T_(1) = M_(1)*(a + u*g) ... Eq1`

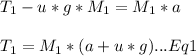
Block 2

`T_(2) - u*g*M_(2) = M_(2) *a \\\\T_(2) = M_(2)*(a + u*g) ... Eq2`

Block 3

`- (T_(1) + T_(2) ) + g*M_(3) = M_(3) *a \\\\T_(1) + T_(2) = M_(3)*( -a + g) ... Eq3`

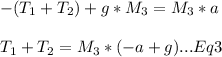
Solving Eq1,2,3 simultaneously

Divide 1 and 2

`(T_(1) )/(T_(2)) = (M_(1)*(a+u*g))/(M_(2)*(a+u*g)) \\\\(T_(1) )/(T_(2)) = (M_(1) )/(M_(2) )\\\\ T_(1) = (M_(1) *T_(2) )/(M_(2) ) .... Eq4`

Put Eq 4 into Eq3

`T_(2) = (M_(3)*(g-a) )/(1+(M_(1) )/(M_(2) ) ) ...Eq5`

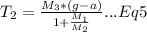
Put Eq 5 into Eq2 and solve for a

`a = (M_(3)*g -u*g*(M_(1) + M_(2)) )/(M_(1) + M_(2) + M_(3) ) .... Eq6`

Substitute back in Eq2 and use Eq4 and solve for T2 & T1

`T_(2) = M_(2)*M_(3)*g*((1-u)/(M_(1) + M_(2)+M_(3)))\\\\T_(1) = M_(1)*M_(3)*g*((1-u)/(M_(1) + M_(2)+M_(3)))\\\\`