Answer:
Explanation:
Let
 .
.
The partial derivatives of this function are
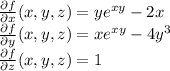
The tangent plane equation through a point
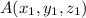 is given by
is given by
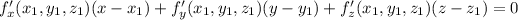
In this case, we have

The values of the partial derivatives in this point are
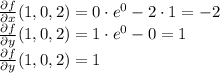
So, the equation is
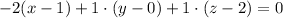
Therefore, the equation for the plane tangent to the surface at the point
 is given by
is given by
