Answer:
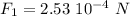
The net force goes to the right
Step-by-step explanation:
Electrostatic Force
Let's consider the situation where 2 point charges q1 and q2 are separated by a distance d. An electrostatic force appears between them whose magnitude can be computed by the Coulomb's formula
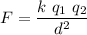
Where k is the constant of proportionality

Two equally-signed charges repel each other, two opposite-signed charges attract each other.
We need to find the total net force exerted on q1 by q2 and q3. We're assuming the charges are placed to the right of the origin, so the distribution is shown in the figure below.
Since q3 repels q1, its force goes to the right, since q2 attracts q1, its force goes to the right also, thus the total force on q1 is :
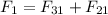
It's directed to the right
Let's compute the individual forces. q3 is separated 2 cm from q1, so d=0.02 m
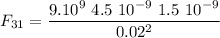
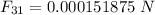
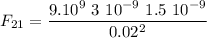
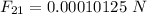

Expressing the force in scientific notation
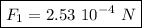
The net force goes to the right