Answer:
The work done by the hoop is equal to 5.529 Joules.
Step-by-step explanation:
Given that,
Mass of the hoop, m = 96 kg
The speed of the center of mass, v = 0.24 m/s
To find,
The work done by the hoop.
Solution,
The initial energy of the hoop is given by the sum of linear kinetic energy and the rotational kinetic energy. So,

I is the moment of inertia,

Since,
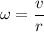
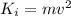
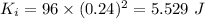
Finally it stops, so the final energy of the hoop will be,
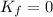
The work done by the hoop is equal to the change in kinetic energy as :
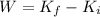
W = -5.529 Joules
So, the work done by the hoop is equal to 5.529 Joules. Therefore, this is the required solution.