Question

At the end of the season, the coach took ten students to burger box.The coach and three students ordered steak-on-a-bun while the other students ordered queen-size burgers. The total bill was $15.15. If a steak-in-a-bun cost $0.90 more than a queen-size burger, find the cost of one of each.

Answer 1

Cost of steak-in-a-bun burger is $1.95 and cost of queen-size burger is $1.05.

Explanation:

Let the cost of queen-size burger be 'q'.

Let the cost of steak-in-a-bun be 's'.

Given:

a steak-in-a-bun cost $0.90 more than a queen-size burger.

So we can say that;

`s=0.9+q \ \ \ \ equation\ 1`

Given:

the coach took ten students to burger box.

Hence Number of person at burger box = 11

The coach and three students ordered steak-on-a-bun while the other students ordered queen-size burgers.

So we can say that;

Number of queen sized burger = 11 - 4 =7

Number of steak on a bun burger = 4

Also Given:

Total bill = $15.11

Now we can say that;

Total bill is equal to sum of Number of queen sized burger multiplied by Cost of queen sized burger and Number of steak on a bun burger multiplied by cost of steak on a bun burger.

framing in equation form we get;

`4s+7q =15.15\ \ \ \ equation\ 2`

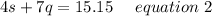
Substituting equation 1 in equation 2 we get;

`4(0.9+q)+7q=15.15`

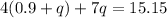
Applying distributive property we get;

`3.6+4q+7q=15.15\\\\3.6+11q=15.15`

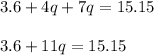
Subtracting both side by 3.6 we get;

`3.6+11q-3.6 =15.15-3.6\\\\11q=11.55`

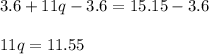
Dividing both side by 11 we get;

`(11q)/(11)=(11.55)/(11)\\\\q=\$1.05`

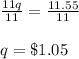
Substituting the value of q in equation 1 we get;

`s=0.9+q=0.9+1.05=\$1.95`

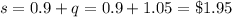
Hence Cost of steak-in-a-bun burger is $1.95 and cost of queen-size burger is $1.05.