Answer:
Cost of steak-in-a-bun burger is $1.95 and cost of queen-size burger is $1.05.
Explanation:
Let the cost of queen-size burger be 'q'.
Let the cost of steak-in-a-bun be 's'.
Given:
a steak-in-a-bun cost $0.90 more than a queen-size burger.
So we can say that;

Given:
the coach took ten students to burger box.
Hence Number of person at burger box = 11
The coach and three students ordered steak-on-a-bun while the other students ordered queen-size burgers.
So we can say that;
Number of queen sized burger = 11 - 4 =7
Number of steak on a bun burger = 4
Also Given:
Total bill = $15.11
Now we can say that;
Total bill is equal to sum of Number of queen sized burger multiplied by Cost of queen sized burger and Number of steak on a bun burger multiplied by cost of steak on a bun burger.
framing in equation form we get;
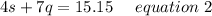
Substituting equation 1 in equation 2 we get;

Applying distributive property we get;
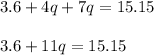
Subtracting both side by 3.6 we get;
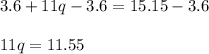
Dividing both side by 11 we get;

Substituting the value of q in equation 1 we get;
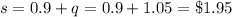
Hence Cost of steak-in-a-bun burger is $1.95 and cost of queen-size burger is $1.05.