Question

Find the value of p and q

Answer 1

Answers: p = 28.36, q = 31.75

values are approximate & rounded to 2 decimal places

===================================================

Work Shown:

tan(angle) = opposite/adjacent

tan(30) = q/55

q = 55*tan(30)

q = 31.7542648054294

q = 31.75

--------

r = 55-p

tan(angle) = opposite/adjacent

tan(50) = q/(55-p)

tan(50) = q/r

tan(50) = 31.7542648054294/r

r*tan(50) = 31.7542648054294

r = 31.7542648054294/tan(50)

r = 26.6449918865414

55-p = 26.6449918865414

-p = 26.6449918865414-55

-p = -28.3550081134586

p = 28.3550081134586

p = 28.36

Answer 2

The answer to your question is p = 27.7 q = 29

Explanation:

Process

1.- Calculate the value of all the angles of the triangle

The angle of 50° and the one to the right are supplementary

x + 50 = 180

x = 130°

- The sum of the internal angles in a triangle equals 180°

30° + y + 130° = 180

y = 180 - 130 - 30

y = 180 - 160

y = 20°

- The angle of the right triangle

50 + 90 + z = 180

z = 180 - 90 - 50

z = 40°

If sum up the superior angles 20 + 40 = 60°, then the biggest triangle is a 30-60-90

2.- Calculate q using the trigonometric function tangent

tan Ф = q / 55

solve for q

q = 55 tan 30

q = 28.9 ≈ 29

3.- Calculate the hypotenuse of the biggest triangle

h² = 55² + 29²

h² = 3866

h = 62,12

4.- Use law of sines to find p

`(p)/(sin 20) = (62.12)/(sin 130)`

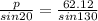
solve for p

p =
`(62.12 sin 20)/(sin 130)`

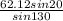
p = 27.74