Answer:
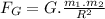 gravitational force
gravitational force
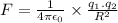 electrostatic force
electrostatic force
Step-by-step explanation:
The forces that balloons may exert on each other can be gravitational pull due to the mass of the balloon membrane and the mass of the gas contained in each. This force is inversely proportional to the square of the radial distance between their center of masses.
The Mutual force of gravitational pull that they exert on each other can be given as:
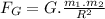
where:
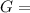 gravitational constant
gravitational constant
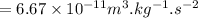
 are the masses of individual balloons
are the masses of individual balloons
 the radial distance between the center of masses of the balloons.
the radial distance between the center of masses of the balloons.
But when there are charges on the balloons, the electrostatic force comes into act which is governed by Coulomb's law.
Given as:
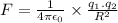
where:
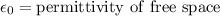
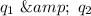 are the charges on the individual balloons
are the charges on the individual balloons
R = radial distance between the charges.