Determine whether each of the following functions is even, odd, or neither even or odd. (a) f(x) = x^5 + x (b) g(x) = 1 - x^6 (c) h(x) = 2x - x^4

Question

asked Nov 19, 2021 176k views

1 Answer

Zack Yoshyaro · Answer 1 · 2021-11-22T18:17:54+0000

Answer with Step-by-step explanation:

Even function: If f(x)=f(-x)

Then, the function is an even function.

Odd function: If
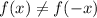
$f(x)\\eq f(-x)$

Then, the function is an odd function.

a.
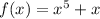
f(x)=x^5+x

Replace x by -x

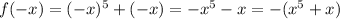
f(-x)=(-x)^5+(-x)=-x^5-x=-(x^5+x)

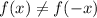
$f(x)\\eq f(-x)$

Hence, the function is an odd function.

b.
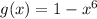
g(x)=1-x^6

Replace x by -x

g(-x)=1-(-x)^6=1-x^6

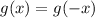
Hence, g(x) is an even function.

c.
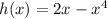
h(x)=2x-x^4

Replace x by -x

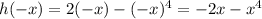
h(-x)=2(-x)-(-x)^4=-2x-x^4

$h(x)\\eq h(-x)$

Hence, h(x) is an odd function.