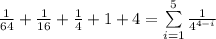Answer:
The given series in sigma notation is
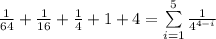
Explanation:
Given series is
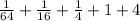
To that given sum expressed in sigma notation :
The given series in sigma notation is
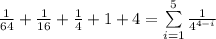
Now check the sigma notation is correct or not:
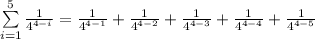
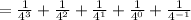
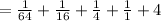
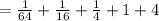
Therefore

Therefore our answer is correct.
The given series in sigma notation is