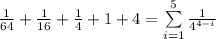Question

How is the sum expressed in sigma notation?

1/64+1/16+1/4+1+4

Answer 1

Explanation:

Answer 2

The given series in sigma notation is

`(1)/(64)+(1)/(16)+(1)/(4)+1+4=\sum\limits_(i=1)^(5)(1)/(4^(4-i))`

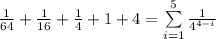
Explanation:

Given series is
`(1)/(64)+(1)/(16)+(1)/(4)+1+4`

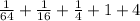
To that given sum expressed in sigma notation :

The given series in sigma notation is

`(1)/(64)+(1)/(16)+(1)/(4)+1+4=\sum\limits_(i=1)^(5)(1)/(4^(4-i))`

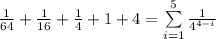
Now check the sigma notation is correct or not:

`\sum\limits_(i=1)^(5)(1)/(4^(4-i))=(1)/(4^(4-1))+(1)/(4^(4-2))+(1)/(4^(4-3))+(1)/(4^(4-4))+(1)/(4^(4-5))`

`=(1)/(4^3)+(1)/(4^2)+(1)/(4^1)+(1)/(4^0)+(1)/(4^(-1))`

`=(1)/(64)+(1)/(16)+(1)/(4)+(1)/(1)+4`

`=(1)/(64)+(1)/(16)+(1)/(4)+1+4`

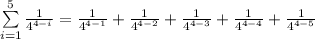
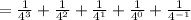
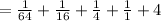
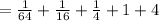
Therefore
`\sum\limits_(i-1)^(5)(1)/(4^(4-i))=(1)/(64)+(1)/(16)+(1)/(4)+1+4`

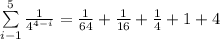
Therefore our answer is correct.

The given series in sigma notation is

`(1)/(64)+(1)/(16)+(1)/(4)+1+4=\sum\limits_(i=1)^(5)(1)/(4^(4-i))`