Answer:
a)
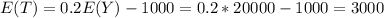
b)
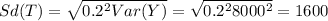
c) Assuming 20 million of families and each one with a mean of income of 20000 for each family approximately then total income would be:
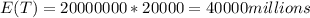
And if we replace into the formula of T we have:
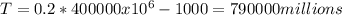
Approximately.
Explanation:
For this case we knwo that Y represenet the random variable "Income" and we have the following properties:
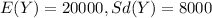
We define a new random variable T "who represent the taxes"
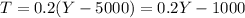
Part a
For this case we need to apply properties of expected value and we have this:
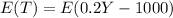
We can distribute the expected value like this:
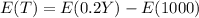
We can take the 0.2 as a factor since is a constant and the expected value of a constant is the same constant.
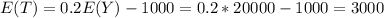
Part b
For this case we need to first find the variance of T we need to remember that if a is a constant and X a random variable

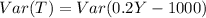
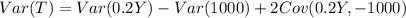
The covariance between a random variable and a constant is 0 and a constant not have variance so then we have this:
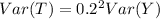
And the deviation would be:
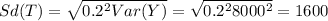
Part c
Assuming 20 million of families and each one with a mean of income of 20000 for each family approximately then total income would be:
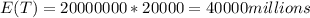
And if we replace into the formula of T we have:
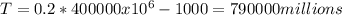
Approximately.