Question

Suppose 0.10 mol of Cu(NO_3)_2 and 1.50 mol of NH_3 are dissolved in water and diluted to a total volume of 1.00 L. Calculate the concentrations of Cu(NH_3)_4^2+ and of Cu^2+ at equilibrium.

Answer 1

To find the equilibrium concentrations, we use the stoichiometry of the reaction between Cu(NO3)2 and NH3. Given the large equilibrium constant, the reaction largely favors the formation of Cu(NH3)42+. We do not have the exact equilibrium constant, but it can be assumed that the concentration of Cu2+ at equilibrium will be small while that of Cu(NH3)42+ will remain close to its initial concentration after reaction with NH3.

Step-by-step explanation:

To calculate the equilibrium concentrations of Cu(NH3)42+ and Cu2+, we start by noting the initial concentrations of Cu(NO3)2 and NH3. Since the reaction stoichiometry is 1:4 for Cu2+ to NH3, we can predict that initially all of the Cu2+ reacts with NH3 to form Cu(NH3)42+. The initial concentration of Cu2+ is 0.10 M and NH3 is 1.50 M. The amount of NH3 required to react with all the Cu2+ is 0.4 M (4 times the moles of Cu2+). This would leave us with 1.10 M NH3 remaining.

Given that the equilibrium constant for the formation of Cu(NH3)42+ is large, we will assume the reaction goes to completion and the initial concentration of Cu(NH3)42+ is 0.10 M. At equilibrium, some of this complex will dissociate back into Cu2+ and NH3. If we let the concentration of dissociated Cu2+ be x, it implies that Cu(NH3)42+ concentration will decrease by x and NH3 concentration will increase by 4x due to the stoichiometry (1:4).

To finalize the calculations, we need the equilibrium constant to calculate the exact value of x. However, with a very large equilibrium constant, x will be very small, and so the equilibrium concentration of Cu2+ (x) will be small, and the concentration of Cu(NH3)42+ will be approximately 0.10 M minus x.

Answer 2

Step-by-step explanation:

It is known that the coefficients change in concentration and in the exponents. Hence, the reaction equation will be as follows.

`Cu^(2+)(aq) + 4NH_(3)(aq) \rightarrow Cu(NH_(3))^(2)_(4)(aq)`

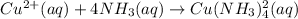
According to the ICE table,

`Cu^(2+)(aq) + 4NH_(3)(aq) \rightarrow Cu(NH_(3))^(2)_(4)(aq)`

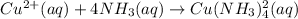
Initial : 0.10 1.50 0

Change : -x -4x +x

Equilibrium: 0.10 - x 1.50 - 4x x

Hence, the mass action expression is as follows.

`K_(f) = ([Cu(NH3)^(2+)_(4)])/([Cu^(2+)][NH_(3)]_(4))`

=
`(x)/((0.10 - x)(1.50 - 4x)^(4))`

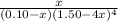
As, the value of is huge, it means that the reaction is very product favored. Hence, we need to find the limiting reactant first and then we get to know what x should be.

In the given reaction ammonia is the limiting reactant, because there is less than 4 times the ammonia as the copper cation. Thus, we expect it to run out first, and so, x is approximately equal to 0.25 M.

So, putting the given values into the above equation as follows.

`1.03 * 10^(13) = (0.25)/((0.10 - 0.25)(1.50 - 4x))^(4)`

=

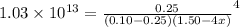
From here

`[NH_(3)] = 1.50 - 4x = ((2.33)/(1.03 * 10^(13)))^{(1)/(4)`

= M

Therefore, we can "re-solve" for x to get and verify that it is still ≈0.250 M.

x =
`[Cu(NH_(3))^(2+)_(4)]`

=
`\frac{1.50 - 2.31284 * 10{-4}}{4}]`

= 0.37491425 M

Thus, we can conclude that concentration of (
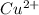`Cu^(2+)`) is 0.37491425 M.