Step-by-step explanation:
It is known that the coefficients change in concentration and in the exponents. Hence, the reaction equation will be as follows.

According to the ICE table,

Initial : 0.10 1.50 0
Change : -x -4x +x
Equilibrium: 0.10 - x 1.50 - 4x x
Hence, the mass action expression is as follows.
![K_(f) = ([Cu(NH3)^(2+)_(4)])/([Cu^(2+)][NH_(3)]_(4))](https://img.qammunity.org/2021/formulas/chemistry/college/yu8wsf0j1mdbl7bwgg603xy31t4yrlgahk.png)
=
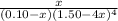
As, the value of is huge, it means that the reaction is very product favored. Hence, we need to find the limiting reactant first and then we get to know what x should be.
In the given reaction ammonia is the limiting reactant, because there is less than 4 times the ammonia as the copper cation. Thus, we expect it to run out first, and so, x is approximately equal to 0.25 M.
So, putting the given values into the above equation as follows.
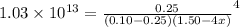
=
From here
![[NH_(3)] = 1.50 - 4x = ((2.33)/(1.03 * 10^(13)))^{(1)/(4)](https://img.qammunity.org/2021/formulas/chemistry/college/lsg2bv7ref3yzno66iyh837350o2f6paiz.png)
= M
Therefore, we can "re-solve" for x to get and verify that it is still ≈0.250 M.
x =
![[Cu(NH_(3))^(2+)_(4)]](https://img.qammunity.org/2021/formulas/chemistry/college/h6aar6mh3qqenb7dfl8gzg6p81cvr2u549.png)
=
![\frac{1.50 - 2.31284 * 10{-4}}{4}]](https://img.qammunity.org/2021/formulas/chemistry/college/16cc6x29id00991d52v0o3w54kmnmt11sd.png)
= 0.37491425 M
Thus, we can conclude that concentration of (
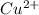 ) is 0.37491425 M.
) is 0.37491425 M.