Question

The numerator and denominator of a fraction are in the ratio of 3 to 5. If the numerator and denominator are both increased by 2, the fraction is now equal to .

If n = the numerator and d = the denominator, which of the following systems of equations could be used to solve the problem?

Answer 1

5n = 3d and 2n – 4 = d – 2 is the answer

Explanation:

Answer 2

Question:

The numerator and denominator of a fraction are in the ratio of 3 to 5. If the numerator and denominator are both decreased by 2, the fraction is now equal to
`(1)/(2)`.

If n = the numerator and d = the denominator, which of the following systems of equations could be used to solve the problem?

5n = 3d and n - 2 = 2d - 4

5n = 3d and 2n - 4 = d - 2

3n = 5d and 2n - 4 = d - 2

Answer:

5n = 3d and 2n – 4 = d – 2

Solution:

Let n be the numerator of the fraction and d be the denominator of the fraction.

Given the numerator and denominator of a fraction are in the ratio of 3 to 5.

This can be written as n : d = 3 : 5.

⇒
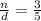`(n)/(d)= (3)/(5)` – – – – (1)

Do cross multiplication, we get

⇒ 5n = 3d

When the numerator and denominator are decreased by 2, the fraction is equal to
`(1)/(2)`.

⇒
`(n-2)/(d-2)= (1)/(2)`

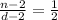
Do cross multiplication, we get

⇒ 2(n –2)=1(d – 2)

⇒ 2n – 4 = d – 2

Hence, 5n = 3d and 2n – 4 = d – 2 can be used to solve the problem.