Answer:
Option 2:
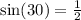
Explanation:
Given:
From the triangle shown below;
A triangle QRS with angle QRS = 90°, ∠QSR = 30°.
Side QR = 5, SQ = 10 and RS = 5√3
Now, we know from trigonometric ratio that,
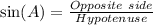
Here, opposite side of angle QSR is QR and Hypotenuse is the side opposite angle QRS which is SQ. Therefore,

Therefore, the value of sine of 30° is one-half. So, second option is correct.