The value of x is
 or
or

Explanation:
The expression is
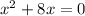
To complete the square, the equation is of the form
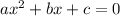
The constant term c can be determined using,
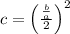
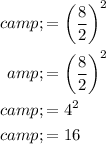
Rewriting the expression
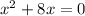 and factoring the trinomial, we have,
and factoring the trinomial, we have,
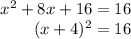
Taking square root on both sides, we get,
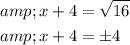
Either,
 or
or
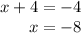
Thus, the value of x is
 or
or
