Question

Complete the square for each expression. Then factor the Trinomial
x^2+8x

Answer 1

The value of x is
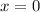`x=0` or
`x=-8`

Explanation:

The expression is
`x^(2) +8x=0`

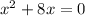
To complete the square, the equation is of the form
`ax^(2) +bx+c=0`

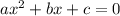
The constant term c can be determined using,
`c=\left(((b)/(a))/(2)\right)^(2)`

`\begin{aligned}c &=\left((8)/(2)\right)^(2) \\&=\left((8)/(2)\right)^(2) \\c &=4^(2) \\c &=16\end{aligned}`

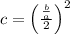
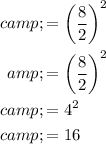
Rewriting the expression
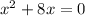`x^(2) +8x=0` and factoring the trinomial, we have,

`\begin{array}{r}{x^(2)+8 x+16=16} \\{(x+4)^(2)=16}\end{array}`

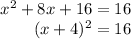
Taking square root on both sides, we get,

`\begin{aligned}&x+4=√(16)\\&x+4=\pm 4\end{aligned}`

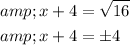
Either,

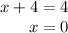`\begin{array}{r}{x+4=4} \\{x=0}\end{array}` or
`\begin{array}{r}{x+4=-4} \\{x=-8}\end{array}`

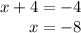
Thus, the value of x is
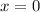`x=0` or
`x=-8`