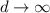Question

Three identical uniform bricks of mass m and length L are stacked on top of each other. (a) What is the maximum distance d so that the stack does not tumble over? (Hint: consider the top two bricks first, then add the bottom brick) (b) What is the maximum distance d that can be achieved by optimal stacking of an infinite number of bricks?

Answer 1

Step-by-step explanation:

Given

Three blocks are placed over each other at a certain distance.

Center of gravity of each block is at distance of 0.5 L from one end of block.

First We consider block 1 and 2

Block 1 center of gravity will try to tumble the block 1 if center of gravity torque goes beyond 0.5 L of second block.

i.e. maximum distance up to which block 1 is placed over block 2 is
`x=0.5 L`

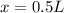
combined center of gravity of 1 and 2 is

Center of gravity
`x=(0.5L+L)/(2)=(3L)/(4)`

Now consider block 2 and 3

Combined center of gravity of block 1 and 2 will tumble over when their Center of gravity goes beyond edge of block 1

i.e. maximum value of
`d=(3L)/(4)`

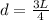
(b) As the no of blocks increases center of gravity increases so maximum value of
`d\rightarrow \infty`