Question

A block of mass 3.1 kg, sliding on a horizontal plane, is released with a velocity of 2.3 m/s. The blocks slides and stops at a distance of 1.9 m beyond the point where it was released.

How far would the block have slid if its initial velocity were quadrupled?

Answer 1

To solve this problem we will apply the concepts given by the kinematic equations of motion. For this purpose it will be necessary with the given data to obtain the deceleration. With this it will be possible again to apply one of the kinematic equations of motion that does not depend on time, but on distance, to find how far the block would slide with the quadruplicate velocity

Our values are given as,

`\text{Initial speed} =V_i = 2.3 m/s`

`\text{Final speed}= V_f = 0 m/s`

`\text{Stopping distance = }d = 1.9 m`

`a = acceleration`

`\text{mass} = m = 3.1kg`

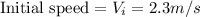
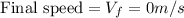
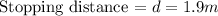
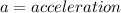
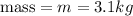
Using the kinematic equation of motion we have

`V_f^2 = V_i^2 + 2 a d`

`0^2 = 2.3^2 + 2 a (1.9)`

`a = -1.39211 m/s^2`

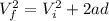
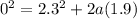
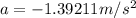
Now if the initial velocity is quadrupled we have that,

`\text{Initial speed} =V_i' = 2.3*4 m/s = 9.2m/s`

`\text{Final speed}= V_f' = 0 m/s`

`\text{Stopping distance = }d'`

`V_f^2' = V_i^2' + 2 a d'`

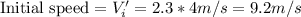
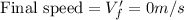
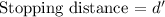
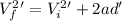
Replacing the values

`0^2 = 9.2^2+ 2 (-1.39211) d'`

`d' = 30.44m`

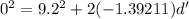
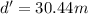
Therefore the block would have slipped around 30.44 if its initial velocity quadrupled.