Question

A transverse wave on a string of amplitude 0.12 m and wavelength 12.16 m propagates with speed 112 m/s. What is the maximum speed a point on the medium moves as this wave passes?

Answer 1

To develop this problem we will start using the concept of maximum speed for this type of systems. The maximum velocity can be described as the product between the Amplitude and the Angular velocity. At the same time, said angular velocity can be found through the relationship between linear and "angular wavenumber" velocity. The Angular wavenumber is a wave number defined as the number of radians per unit distance. Finally with the value of the angular velocity found we will proceed to find the maximum speed.

The maximum speed is given by

`v_(max) = A\omega`

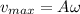
Here,

A = Amplitude

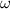`\omega`= Angular velocity

The angular velocity can be described as the number of radians per unit distance

`\omega = vk`

`\omega = v ((2\pi)/(\lambda))`

`\omega = 112((2\pi)/(12.16))`

`\omega =57.8714rad/s`

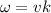
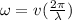
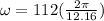
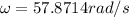
Then,

`v_(max) = 0.12 *57.8714`

`v_(max) = 6.94m/s`

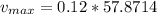
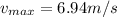
Therefore the maximum speed a point on the medium moves as this wave passes is 6.94m/s