To develop this problem we will start using the concept of maximum speed for this type of systems. The maximum velocity can be described as the product between the Amplitude and the Angular velocity. At the same time, said angular velocity can be found through the relationship between linear and "angular wavenumber" velocity. The Angular wavenumber is a wave number defined as the number of radians per unit distance. Finally with the value of the angular velocity found we will proceed to find the maximum speed.
The maximum speed is given by
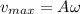
Here,
A = Amplitude
 = Angular velocity
= Angular velocity
The angular velocity can be described as the number of radians per unit distance
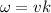

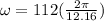
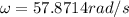
Then,
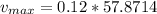
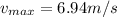
Therefore the maximum speed a point on the medium moves as this wave passes is 6.94m/s