Question

The graph plots four equations, A, B, C, and D: Line A joins ordered pair negative 6, 16 and 9, negative 4. Line B joins ordered pair negative 2, 20 and 8, 0. Line C joins ordered pair negative 7, negative 6 and 6, 20. Line D joins ordered pair 7, 20 and 0, negative 7.

Which pair of equations has (2, 12) as its solution? (4 points)

Equation A and Equation C
Equation B and Equation C
Equation C and Equation D
Equation B and Equation D

Answer 1

The pair of equations which has (2,12) as its solution is,

equation B and equation C.

Explanation:

According to the question,

equation of line A is
`\frac {y - 16}{x + 6} = \frac {16 + 4}{-6 - 9}`

or,
`\frac {y - 16}{x + 6} = \frac {-4}{3}`

or,
`3y - 48 = -4x - 24`

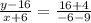
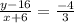
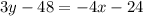
or, 3y + 4x = 24 ------------------(1)

Now, the point (2, 12) doesn't satisfy (1). Hence, (2,12) is not a solution for the line A.

Equation of line B is,
`\frac {y - 20}{x + 2} = \frac {20 - 0}{-2 - 8}`

or,
`\frac {y - 20}{x + 2} = -2`

or,
`y - 20 = -2x  - 4`

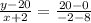
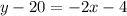
or, y + 2x = 16 -----------------------------(2)

The point (2,12) is satisfied by (2). Hence, (2, 12) is a solution for line B.

Equation of line C is,
`\frac {y + 6}{x + 7} = \frac {20 + 6}{6 + 7}`

or,
`\frac {y + 6}{x + 7} = 2`

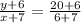
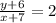
or, y + 6 = 2x + 14

or. y - 2x = 8 -----------------------------------(3)

The point (2, 12) is satisfied by (3). Hence, (2 , 12) is a solution for the line C.

Equation of line D is,
`\frac {y - 20}{x - 7} =\frac {20 + 7}{7 - 0}`

or,
`\frac {y - 20}{x - 7} = \frac {27}{7}`

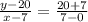
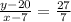
or, 7y - 140 = 27x - 189

or, 7y - 27x = -49----------------------------------------(4)

The point (2, 12) is not satisfied by (4). hence, (2, 12) is not a solution of the line D

Hence, the pair of equations which has (2,12) as its solution is,

equation B and equation C.