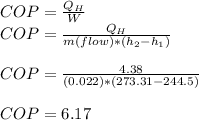Answer:
a) 0.813
b) 4.38 KW
c) COP = 5.13
d) 3.91 KW , COP = 6.17
Step-by-step explanation:
Data obtained A-13 tables for R-134a:
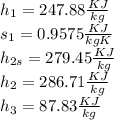
The isentropic efficiency of the compressor is determined by :
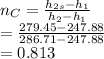
The rate of heat supplied to the room is determined by heat balance:
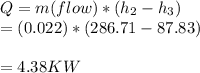
Calculating COP
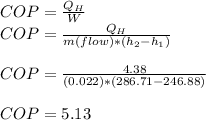
Part D
Data Obtained:
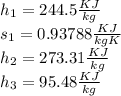
The rate of heat supplied to the room is determined by heat balance:
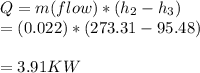
Calculating COP