Question

There are two major cell phone providers in the Colorado Springs, Colorado area, one called HTC and the other, Mountain Communications. We want to investigate the "churn rate" for each provider. Churn is the amount of customers or subscribers who cut ties with a company during a given time period. At the beginning of the month, HTC had 10,000 customers; at the end of the month, HTC had 9810 customers for a loss of 190. For the same month, Mountain Communications started with 12,500 customers and ended the month with 12,285 customers, for a loss of 215. At the 0.01 significance level, is there a difference in the churn rate for the two providers?

Answer 1

Explanation:

Hello!

The objective of this exercise is to compare the "Churn rate" between the two major cell phone providers in colorado springs.

For each provider, the number of subscribers was noted at the beginning and end of a month.

The study variables are:

X₁: Number of customers that cut ties with HTC over a month.

X₂: Number of customers that cut ties with Mountain Communications over a month.

To compare the churn rate of both companies, the parameters of interest are the population proportions of customers that stopped using the companies services over the given period.

The hypotheses of interest are:

H₀: p₁ = p₂

H₁: p₁ ≠ p₂

α: 0.01

The statistic to use is the standard normal approximation:

`Z= \frac{('p_1-'p_2)- (p_1-p_2)}{\sqrt{'p(1 - 'p)[(1)/(n_1) + (1)/(n_2) ]} } }`

Z≈N(0;1)

HTC

n₁= 10000 customers (beginning of the month)

x₁= 190 customers (people that stopped using the company service)

sample proportion 'p₁= x₁/n₁= 190/10000= 0.019

Mountain Communications

n₂= 12285 customers (beginning of the month)

x₂= 215 customers (people that stopped using the company service)

sample proportion 'p₂= x₂/n₂= 215/12285= 0.0175

pooled sample proportion
`'p= (x_1 + x_2)/(n_1 + n_2) = (190 + 215)/(10000 + 12285)`

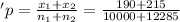
'p= 0.0182

`Z_(H_0)= \frac{(0.019 - 0.0175) - 0}{\sqrt{(0.0182*0.9818)[(1)/(10000) + (1)/(12285) ]} }`

`Z_(H_0)= 0.833`

The p-value for this test is: 0 .4048

Note: Using the p-value method to decide over a hypothesis test, the decision rule is:

If p-value ≥ α, then you do not reject the null hypothesis.

If p-value < α, then you reject the null hypothesis.

The p-value < α, so the decision is to reject the null hypothesis.

With a significance level of 1%, there is enough evidence to conclude that there is a difference between the churn rate of the two cell phone providers.

I hope it helps!