Question

The turbine develops 300 kW of power, which is transmitted to the gears such that both B and C receive an equal amount. If the rotation of the 100-mm-diameter A992 steel shaft is v = 600 rev>min., determine the absolute maximum shear stress in the shaft and the rotation of end D of the shaft relative to A. The journal bearing at D allows the shaft to turn freely about its axis.

Answer 1

2387350 Nm

0.929 degrees

Step-by-step explanation:

w = 2*pi*f = 2*pi*600/60 = 62.831 rad/s

Given data:

P = 300*10^3 W ; G = 75 GPa ; d = 0.1m ; r = 0.05m

`J = (pi * c^4)/(2) = (pi * r^4)/(2) = (pi * 0.05^4)/(2) = 9.8175*10^(-6) m^4\\\\T = (P)/(w) = (300,000)/(62.831) = 4774710 Nm\\\\TC = TB = 0.5*T = 2387350 Nm\\`

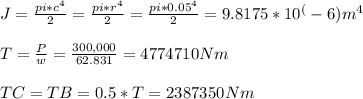
Tmax is the torque at any point of part AB and is equal to T generated at point A, and from B to D the power and torque will be removed by gears.

`t_(max) = (T*r)/(J) = (4774710*0.05)/(9.8175*10^(-6))=24.3MPa\\\\Q_(D/A) = sum ((T*L)/(J*G)) = (TAB*LAB)/(J*G) + (TBC*LBC)/(J*G) \\\\= (4774710*1.5)/((9.8175*10^(-6)) * 79 * 10^9) + (2387350*2)/((9.8175*10^(-6)) * 79 * 10^9)\\\\= 0.01621 rad\\\\Q_(D/A) = 0.01621 * (180)/(pi) = 0.929 degrees`