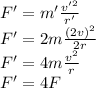Question

An astronaut in an orbiting space craft attaches a mass m to a string and whirls it around in uniform circular motion. The radius of the circle is R, the speed of the mass is v, and the tension in the string is F. If the mass, radius, and speed were all to double the tension required to maintain uniform circular motion would be

Answer 1

`F'=4F`

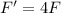
Step-by-step explanation:

According to Newton's second law, the tension in the string is equal to the centripetal force, since the mass is under an uniform circular motion:

`F=F_c\\F=ma_c`

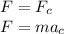
Here
`a_c` is the centripetal acceleration, which is defined as:

`a_c=(v^2)/(r)`

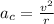
So, replacing:

`F=m(v^2)/(r)`

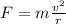
In this case we have
`m'=2m`,
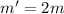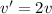`v'=2v` and
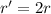`r'=2r`. Thus, the tension required to mantain uniform circular motion is:

`F'=m'(v'^2)/(r')\\F'=2m((2v)^2)/(2r)\\F'=4m(v^2)/(r)\\F'=4F`