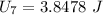Answer:
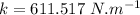
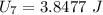
Step-by-step explanation:
Given:
- spring potential energy stored due to hanging mass,

- mass attached to the spring,
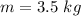
Now the force on the mass due to gravity:
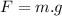
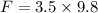
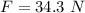
This force pulls the spring down, so:
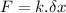
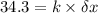 ....................(1)
....................(1)
For the spring potential:

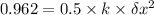
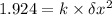 .........................(2)
.........................(2)
Using eq. (1) & (2)
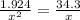
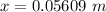
a.
Now the spring factor:
using eq. (1)

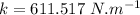
b.
when mass attached is 7 kg.
The spring potential energy:
 ............(3)
............(3)
Now the force on the mass due to gravity:
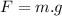
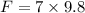
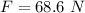
This force pulls the spring down, so:
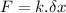

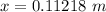
Using eq. (3)