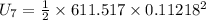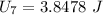Question

A vertical spring stores 0.962 J in spring potential energy whena 3.5-kg mass is suspended from it.(a)by what multiplicative factordoes the spring potential energy change if the mass atttached tothe spring is doubled?(b)verify your answer to part (a)bycalculating the spring potential energy when a 7.0-kg mass isattached to the spring.

Answer 1

`k=611.517\ N.m^(-1)`

`U_7=3.8477\ J`

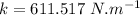
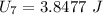
Step-by-step explanation:

Given:

• spring potential energy stored due to hanging mass,
  `U=0.962\ J`

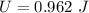
• mass attached to the spring,
  `m=3.5\ kg`

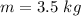
Now the force on the mass due to gravity:

`F=m.g`

`F=3.5 * 9.8`

`F=34.3\ N`

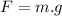
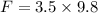
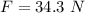
This force pulls the spring down, so:

`F=k.\delta x`

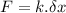
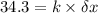`34.3=k* \delta x` ....................(1)

For the spring potential:

`U=(1)/(2) k.\delta x^2`

`0.962=0.5* k* \delta x^2`

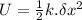
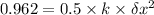
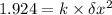`1.924=k* \delta x^2` .........................(2)

Using eq. (1) & (2)

`(1.924)/(x^2) =(34.3)/(x)`

`x=0.05609\ m`

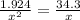
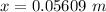
a.

Now the spring factor:

using eq. (1)

`34.3=k* \delta 0.05609`

`k=611.517\ N.m^(-1)`

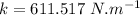
b.

when mass attached is 7 kg.

The spring potential energy:

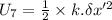`U_7=(1)/(2) * k.\delta x'^2` ............(3)

Now the force on the mass due to gravity:

`F=m.g`

`F=7* 9.8`

`F=68.6\ N`

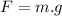
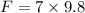
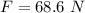
This force pulls the spring down, so:

`F=k.\delta x`

`68.6=611.517* \delta x`

`x=0.11218\ m`

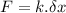
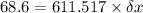
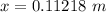
Using eq. (3)

`U_7=(1)/(2)* 611.517* 0.11218^2`

`U_7=3.8478\ J`

Answer 2

a) If the mass get double then the potential of the spring gets four times.

b) P'=3.848 J

Step-by-step explanation:

Given that

P= 0.962 J

m = 3.5 kg

m'= 7 kg

Lets take extension in the spring is x when the mass 3.5 kg is attached to the spring.

m g = K x

K=Spring constant

`x=(mg)/(K)`

We know that potential energy given as

`P=(1)/(2)Kx^2`

`P=(1)/(2)K* (m^2g^2)/(K^2)`

`P=(1)/(2)* (m^2g^2)/(K)`

If the mass get double then the potential of the spring gets four times.

`P'=(1)/(2)* ((2m)^2g^2)/(K)`

`P'=4* (1)/(2)* (m^2g^2)/(K)`

P'= 4 P

When mass ,m' = 7 kg

Then potential will be

`0.962=(1)/(2)* (3.5^2* g^2)/(K)` -----1

`P'=(1)/(2)* (7^2* g^2)/(K)` -------2

From equation 1 and 2

`(0.962)/(P')=((1)/(2)* (3.5^2* g^2)/(K) )/((1)/(2)* (7^2* g^2)/(K) )`

P'= 4 x 0.962 J

P'=3.848 J