Question

A consumer advocate claims that 80 percent of cable television subscribers are not satisfied with their cable service. In an attempt to justify this claim, a randomly selected sample of cable subscribers will be polled on this issue. (a) Suppose that the advocate's claim is true, and suppose that a random sample of 7 cable subscribers is selected. Assuming independence, use an appropriate formula to compute the probability that 5 or more subscribers in the sample are not satisfied with their service. (Do not round intermediate calculations. Round final answer to p in 2 decimal place. Round other final answers to 4 decimal places.) Binomial, n

Answer 1

Answer: 0.8520

Explanation:

Given : The probability that cable television subscribers are not satisfied with their cable service is 80%=0.80.

We assume that each subscriber is independent from each other, so we can apply Binomial distribution.

In binomial distribution, the probability of getting success in x trials is given by :-

`P(X=x)=^nC_xp^x(1-p)^(n-x)`

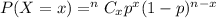
, where n is the total number of trials , p is the probability of getting success in each trial .

Let x be the number of subscribers in the sample are not satisfied with their service..

So, p=0.8

Sample size : n=7

The probability that 5 or more subscribers in the sample are not satisfied with their service will be :-

`P(x\geq5)=P(5)+P(6)+P(7)\\\\=^7C_5(0.8)^5(0.2)^2+^7C_6(0.8)^6(0.2)^1+^7C_7(0.8)^7(0.2)^0\\\\=(7!)/(5!(7-5)!)(0.0131072)+(7)(0.0524288)+(1)(0.2097152)\ \[\because\ ^nc_r=(n!)/(r!(n-r)!)]\\\\=0.2752512+0.3670016+0.2097152\\\\=0.851968\approx0.8520`

Hence, the probability that 5 or more subscribers in the sample are not satisfied with their service is 0.8520 .