Answer: 0.8520
Explanation:
Given : The probability that cable television subscribers are not satisfied with their cable service is 80%=0.80.
We assume that each subscriber is independent from each other, so we can apply Binomial distribution.
In binomial distribution, the probability of getting success in x trials is given by :-
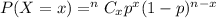
, where n is the total number of trials , p is the probability of getting success in each trial .
Let x be the number of subscribers in the sample are not satisfied with their service..
So, p=0.8
Sample size : n=7
The probability that 5 or more subscribers in the sample are not satisfied with their service will be :-
![P(x\geq5)=P(5)+P(6)+P(7)\\\\=^7C_5(0.8)^5(0.2)^2+^7C_6(0.8)^6(0.2)^1+^7C_7(0.8)^7(0.2)^0\\\\=(7!)/(5!(7-5)!)(0.0131072)+(7)(0.0524288)+(1)(0.2097152)\ \[\because\ ^nc_r=(n!)/(r!(n-r)!)]\\\\=0.2752512+0.3670016+0.2097152\\\\=0.851968\approx0.8520](https://img.qammunity.org/2021/formulas/mathematics/college/gci0c0g57f7h5707dpx6rl2sir98ajby80.png)
Hence, the probability that 5 or more subscribers in the sample are not satisfied with their service is 0.8520 .