Answer:
Therefore,
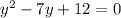 ....Standard form.
....Standard form.
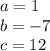 ......Numerical Coefficients.
......Numerical Coefficients.
Explanation:
Given:
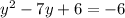
To Find:
a ,b , c
Solution:
Quadratic:
A quadratic equation is an equation of the second degree.
Meaning it contains at least one term that is squared.
The standard form is ax² + bx + c = 0 with a, b, and c being constants, or numerical coefficients, and x is an unknown variable.
Here it is given as
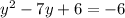
Adding 6 on both the side we get
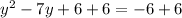
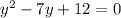
Which is Quadratic Equation in STANDARD form Where,
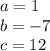
Therefore,
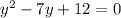 ....Standard form.
....Standard form.
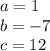 ......Numerical Coefficients.
......Numerical Coefficients.