Answer:
- 60th term of sequence is 420
Explanation:
In this question we have given a sequence or you can say it arithmetic progression which is 7 , 14 , 21,.. and we have asked to find it's 60th term .
From sequence 7 , 14 , 21.... :
- d = common difference = 14 - 7 = 7
As we know that :
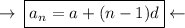
Where ,
- n refers to number of term
- d refers to common difference
Now , substituting values :
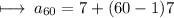
Now , calculating :
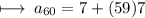
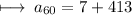
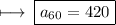
- Therefore , value of 60th term of the given sequence is 420 .
#Keep Learning