Answer:
Mass, m = 2.2 kg
Step-by-step explanation:
It is given that,
Frequency of the piano, f = 440 Hz
Length of the piano, L = 38.9 cm = 0.389 m
Tension in the spring, T = 667 N
The frequency in the spring is given by :
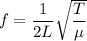
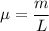 is the linear mass density
is the linear mass density
On rearranging, we get the value of m as follows :
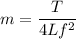
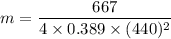
m = 0.0022 kg
or
m = 2.2 grams
So, the mass of the object is 2.2 grams. Hence, this is the required solution.