Answer:
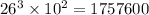
option B is correct
Explanation:
We have 5 spaces in the license plate:
_ _ _ _ _
we have 26 available letters, and 10 available numbers.
starting with letters:
- how many choices do i have to place the 1st letter? 26.
26 _ _ _ _
- how many choices do i have to place the 2nd letter? 26 (since we're allowed to repeat letters)
26 26 _ _ _
- how many choices do i have to place the 3rd letter? 26
26 26 26 _ _
we've used all the places for letters, (note: the exact position of the letters doesn't matter here, the first letter could've been placed anywhere in _ _ _ _ _, but the amount of possible choices for letters would always be 26).
let's move on to numbers.
- how many choices do i have to place the 1st number? 10
26 26 26 10 _
- how many choices do i have to place the 2nd number? 10
26 26 26 10 10
we've completed our number plate. Next we'll simply multiply all these numbers to get all the possible arrangements in which numbers and letters can be displayed on a license place.
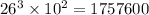
option B is correct