Question

The altitude to the hypotenuse of a right triangle divides the hypotenuse into segments with lengths in the ratio 1 : 2. The length of the altitude is 8. How long is the hypotenuse?

a. 16

b. 24

c.
`4√(2)`

d.
`6√(6)`

Answer 1

a) The length of the hypotenuse = 16 units.

Explanation:

Here, let us assume the given right angle triangle is Δ ABC.

Here. AC is the hypotenuse, which is divided in the ratio 1: 2 by the altitude BM.

⇒ AM : MC = 1: 2

Let us assume the common ratio = x

⇒ AM = x and MC = 2 x

Also. AM = 8 units

Solving this by common ratio of sides, we get:

`\implies (2x)/(x) = (x)/(8) \\\implies 2x^2 = 64\\\implies x^2 = 32\\\implies x = 4\sqrt 2`

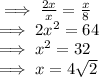
Hence, AM = 4√2 , MC = 2 (4√2)

⇒ AC = 12√2 units ≈ 16 units

Hence, the length of the hypotenuse = 16 units.