The length of side of cube is
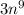 units
units
Solution:
Given that, volume of cube is
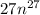 cubic units
cubic units
To find: length of one side of cube
The volume of a cube is given as:

Where, "a" is the length of side of cube
Substituting the given value of volume we get,
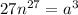 ------ eqn 1
------ eqn 1
We know that,
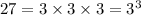
Substitute the above in eqn 1
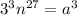
Now again substitute for 27 = 3 x 9
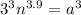
Take 3 as common power

By taking cube roots on both side,
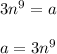
Thus length of side of cube is
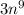 units
units