Given
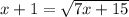
We have to set the restraint
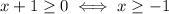
because a square root is non-negative, and thus it can't equal a negative number. With this in mind, we can square both sides:
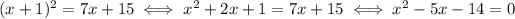
The solutions to this equation are 7 and -2. Recalling that we can only accept solutions greater than or equal to -1, 7 is a feasible solution, while -2 is extraneous.
Similarly, we have
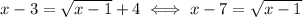
So, we have to impose

Squaring both sides, we have
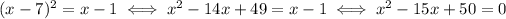
The solutions to this equation are 5 and 10. Since we only accept solutions greater than or equal to 7, 10 is a feasible solution, while 5 is extraneous.