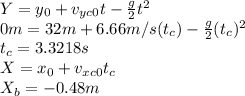Question

A 9.8 kg firework is launched straight up and at its maximum height 32 m it explodes into three parts. Part A (0.5 kg) moves straight down and lands 0.27 seconds after the explosion. Part B (0.5 kg) moves horizontally to the right and lands 6.5 meters from Part A. Part C moves to the left at some angle. How far from Part A does Part C land (no direction needed)?

Answer 1

The part c land 0.48m apart from the part a.

Step-by-step explanation:

This can be solve using conservation of linear momentum. The explosion can be considered as an explosive collision, in which the internal forces are far stronger than the external ones. therefore we can consider the external forces as insignificant. In this case, the linear momentum before and after the explosion is the same. Therefore:

`\vec{P}_(tot0)=\vec{P}_(a)+\vec{P}_(b)+\vec{P}_(c)`

The final speed of the firework was 0m/s (maximum height), therefore its momentum P was null before the explosion. This means:

`0N/s=\vec{P}_(a)+\vec{P}_(b)+\vec{P}_(c)`

`\left \{ {{P_(ya)+P_(yc)=0} \atop {P_(xb)+P_(xc)=0}} \right.`

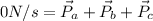
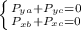
The total mass of the firework was 9.8kg, therefore the mass of part c is:

mc=Mtot-ma-mb=8.8kg

Now we have to calculate the initial speed of part a and part b. For both, we can use Vertical Projectile Motion equations:

For A:

`Y=y_0+v_(ay0)t-(g)/(2)t^2\\ 0m=32m+v_(b0)(0.27s)-(g)/(2)(0.27s)^2\\v_(ay0)=-117.19m/s`

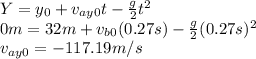
For B:

`Y=y_0+v_(yb0)t-(g)/(2)t^2\\ 0m=32m+0m/s(t_b)-(g)/(2)(t_b)^2\\t_(b)=2.554s\\X=x_0+v_(xb0)t_b\\6.5m=0m+v_(xb0)\cdot 2.554s\\v_(xb0)=2.54m/s`

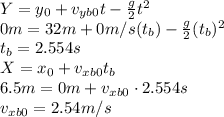
Using the conservation of linear momentum, we calculate the speed of C:

`\left \{ {{P_(ya)+P_(yc)=0} \atop {P_(xb)+P_(xc)=0}} \right.\\P_(ya)+P_(yc)=m_av_(ay0)+m_cv_(cy0)=0 \rightarrow v_(cy0)=6.66m/s\\P_(xb)+P_(xc)=0=m_bv_(bx0)+m_cv_(cx0) \rightarrow v_(cx0)=-0.1445m/s`

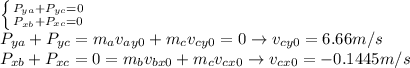
Using now Vertical Projectile Motion for part C:

`Y=y_0+v_(yc0)t-(g)/(2)t^2\\ 0m=32m+6.66m/s(t_c)-(g)/(2)(t_c)^2\\t_(c)=3.3218s\\X=x_0+v_(xc0)t_c\\X_(b)=-0.48m`

Answer 2

s=0.36m part c lands

Step-by-step explanation:

from conservation of linear momentum

we know that

the momentum before Collision(explosion) is equal to the momentum after collision( explosion)

0=maua+mbub+mcuc

ma=.5kg

mb=.5kg

mc=9.8-(0.5+0.5)

mc=8.8kg

since the fragments all fall to the ground at the same time, we assume same time for all

t=0.27s

the velocity of a

v=u +at

since it falling stariaght down

v=0+9.81*.27

v=2.64m/s is the vertical side of its velocity

, since its falling straight down , the horizontal velocity is zero

the velocity of b

s=ut horizontal component of the distance

6.5=.27*ub

ub=24.07m/s

from

0=maua+mbub+mcuc

0=0.5*0+0.5*24.07+8.8*cu

uc=1.36

the distance from a will be

s=ut

s=1.36*.27

s=0.36m