Answer:
10! = 3628800 ways
Explanation:
Some interesting points
This is a problem of permutations where, at the time of forming different groups, the order of the elements matters but none of them can appear more than once in the same group (no repetition is allowed).
Order matters in the sense that you can form different groups when one element of it changes its position. For instance, suppose having a group of ten students, like the case in the question, whose names are:
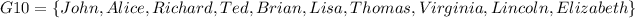
Then, if we change one student from one position to another---order matters---we have a different group, a permutation, another way of lining them up, like the next one:
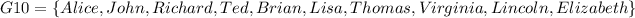 or
or
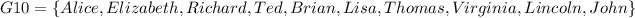
And so on. Notice that in the file does not appear the same person more than once. In this real case, it is impossible to have the same person twice in the file, so that restriction is perfectly described using permutations.
Solving the question
We can say that we first have ten (10) possible students for occupying the first place. After that, remains nine (9) of them for being in this ninth place, and so on for
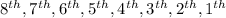 places.
places.
After knowing this, we need to apply the Multiplication Principle, which roughly says that if we have m possibilities for doing any action and n possibilities for doing another action, then, there are m * n ways of performing both actions.
We can express the former reasons mathematically as follows:
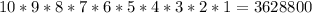 ways of lining up ten different students in a file.
ways of lining up ten different students in a file.
Notice that
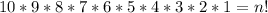 , which is the factorial of n.
, which is the factorial of n.