Question

What is the length of side a? Round to the nearest tenth

Answer 1

○
`\displaystyle 12,9`

Step-by-step Step-by-step explanation:

Use the Law of Sines to find the length of the second edge:

Solving for Angles

`\displaystyle \frac{sin\angle{C}}{c} = \frac{sin\angle{B}}{b} = \frac{sin\angle{A}}{a}`

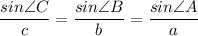
Use
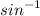`\displaystyle sin^(-1)`towards the end or you will throw your result off!

Solving for Edges

`\displaystyle \frac{c}{sin\angle{C}} = \frac{b}{sin\angle{B}} = \frac{a}{sin\angle{A}}`

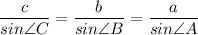
Let us get to wourk:

`\displaystyle (a)/(sin\:40) = (10)/(sin\:30) \hookrightarrow (10sin\:40)/(sin\:30) = x; 12,855752194... \\ \\ \boxed{12,9 \approx x}`

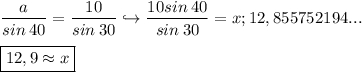
I am joyous to assist you at any time.