Answer:
0.34148 m
Step-by-step explanation:
 = Resistivity of tungsten =
= Resistivity of tungsten =
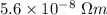
d = Diameter = 0.0018 inch
r = Radius =
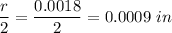
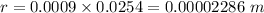
 = Temperature coefficient of tungsten =
= Temperature coefficient of tungsten =

Power is given by

We have the equation
![R_2=R_1[1+\alpha(T_2-T_1)]\\\Rightarrow R_1=(R_2)/(1+\alpha(T_2-T_1))\\\Rightarrow R_1=(144)/(1+0.0045(2550-25))\\\Rightarrow R_1=11.64812\ \Omega](https://img.qammunity.org/2021/formulas/physics/college/o8nldhfg0ld9irg7wpi46tzkldgqf8s5iu.png)
Resistance is given by

The length of the filament is 0.34148 m